Turunan fungsi Aljabar
Pengertian Turunan Fungsi Aljabar
Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi.
Notasi turunan fungsi aljabar seperti berikut:
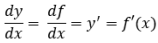
Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut:
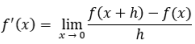
Rumus Turunan Aljabar
Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut:
Turunan Fungsi Pangkat

Turunan Hasil Kali Fungsi
Bentuk dari fungsi kali adalah f(x) = u(x) . v(x), sehingga turunannya adalah f’(x) = u’(x)v(x) + u(x)v’(x).
Contoh Soal:

Turunan Fungsi Pembagian

Contoh Soal:

Turunan Pangkat dari Fungsi

Contoh Soal:

Turunan Trigonometri
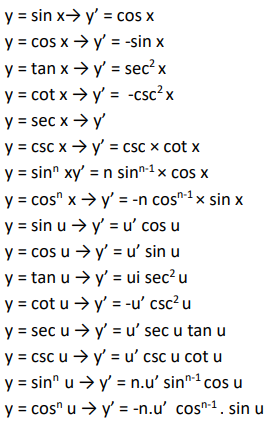
Bagaimana, Sobat Pintar?
Apa sudah mulai mengerti rumus-rumus dari turunan fungsi aljabar?
Rumus-rumus di atas perlu kalian pahami agar dapat menyelesaikan permasalahan yang berkaitan dengan turunan fungsi aljabar
Persamaan Garis Singgung Kurva

Garis singgung bergradien m, jika titik yang dilaluinya adalah titik singgung A(x1,y1) maka persamaan garis singgungnya adalah

Persamaan garis normal bergradien -1/m dan melalui A(x1,y1)

Untuk memperjelas persamaan garis singgung dan garis normal, ikuti simulasi berikut ini:
Apakah Anda sudah memahami persamaan garis singgung dan persamaan garis normal di titik tertentu pada kurva? Jika belum, Anda dapat mengamati kembali animasi tentang persamaan garis singgung dan persamaan garis normal. Selanjutnya, cobalah pahami contoh persamaan garis singgung dan garis normal berikut ini.
Contoh
Tentukan Persamaan garis singgung dan garis normal pada kurva y = x4 - 7x2 + 20 di titik yang berabsis 2 adalah...
Jawab :
x = 2 y = x4 - 7x2 + 20 ⟶ y = 24 - 7.22 + 20 = 16 - 28 + 20 = 8 titik singgung A(2,8)
Persamaan Garis singgung
m = y' = 4x3 - 14 x = 4.23 - 14.2 = 32 - 28 = 4 , gradien, m = 4 melalui A(2,8)
Jadi, persamaan garis singgungnya adalah
y - y1 = m(x - x1)
y - 8 = 4(x - 2)
y - 8 = 4x - 8
y = 4x ⟶ Persamaan garis singgung
Persamaan garis normal
gradien garis singgung , m = 4, gradien garis normal m2 = - 1/4
Garis normal bergardien m2 = - 1/4 melalui A(2,8)
Jadi, persamaan garis Normalnya adalah
y - y1 = m2(x - x1)
y - 8 = - 1/4(x - 2) kalikan 4
4y - 32 = -x +2
x + 4y = 34 ⟶ Persamaan garis normal
2. Tentukan persamaan garis singgung kurva y = x2 di titik (-1, 1)!
Jawab:
Cari gradien dari kurva y dengan menggunakan turunan pertama. m = y’
m = f '(a)
= 2x
m = 2(-1)
= -2
Maka persamaan garis singgung kurva dengan gradient m = -2 di titik (-1, 1) adalah
y -y1 = m(x -x1)
y -1 = -2(x-(-1))
y -1 = -2x -2
y = -2x -1
Aplikasi Turunan
Setelah mempelajari tentang rumus-rumus turunan, Sobat Pintar juga perlu mempelajari mengenai penerapan turunan. Ternyata turunan juga bisa diterapkan dalam materi yang lain. Beberapa penerapan turunan fungsi, yaitu :
1. Gradien Persamaan Garis Singgung
Salah satu cara untuk membuat sebuah persamaan garis singgung adalah dengan menggunakan gradien atau kemiringan dari garis tersebut. Gradien suatu fungsi f(x) yang melalui titik A (a,f(a)) dapat ditentukan dengan menggunakan turunan dengan rumus: m = f’(a).
2. Kemonotonan Fungsi
Aplikasi turunan yang lainnya adalah menentukan kemonotonan suatu fungsi. Maksudnya, Sobat pintar dapat mengetahui suatu fungsi naik atau turun pada interval tertentu.

3. Titik Stasioner
Titik stasioner disebut juga titik kritis, titik ekstrim, atau titik balik. Titik stasioner merupakan sebuah titik pada kurva dengan gradien dari garis singgung kurva bernilai 0 (nol).
Jika fungsi f(x) kontinu dan terdiferensial, maka f(a) dikatakan NILAI STASIONER dari f(x) jika dan hanya jika f’(a)=0.
4. Nilai Maksimum dan Minimum Fungsi
Sebelum menentukan nilai maksimum dan minimum, Sobat Pintar harus tahu cara menentukan titik maksimum dan minimum terlebih dahulu.
Titik maksimum atau minimum suatu fungsi f(x) pada interval [a,b] dapat ditentukan dengan langkah-langkah berikut:
1). Penuhi syarat nilai stasioner, yaitu f’(a) = 0 dan f’(b) = 0
2). Tentukan jenis stasionernya (titik maksimum, titik belok, atau titik minimum) dengan menggunakan turunan kedua fungsi tersebut, yaitu:
- Jika f’’(a) < 0 maka f(a) adalah nilai balik maksimum fungsi f
- Jika f’’(a) > 0 maka f(a) adalah nilai balik minimum fungsi f
- Jika f’’(a) = 0 maka f(a) bukan nilai ekstrim fungsi f
3). Substitusi nilai variabelnya ke fungsi awal, sehingga diperoleh nilai maksimum atau minimumnya.
Nilai maksimum atau minimum suatu fungsi yang kontinu dan diferensiabel pada setiap titik di interval [a,b] dapat terjadi pada:
- Titik stasioner yang berada pada interval [a,b]
- Titik ujung interval
Dalam menentukan nilai maksimum atau minimum suatu fungsi dapat dilakukan melalui langkah-langkah berikut:
1). Menentukan titik stasioner pada fungsi f(x) yang berada pada interval [a,b]
2). Menentukan nilai fungsi pada ujung interval, yaitu f(a) dan f(b)
3). Membandingkan nilai fungsi pada langkah 1 dan 2. Nilai yang terbesar adalah nilai maksimum, sedangkan nilai terkecil adalah nilai minimum
5. Kecepatan dan Percepatan Benda
Wah, nggak nyangka ya, ternyata turunan juga digunakan dalam rumus Fisika yang sering kita jumpai, yaitu kecepatan dan percepatan.
Jika diketahui sebuah benda bergerak menempuh jarak s = f(t), maka kecepatan dan percepatan benda tersebut dapat dirumuskan sebagai berikut:
- Kecepatan benda saat t detik (turunan pertama). Rumus turunan pertama yaitu:
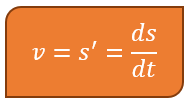
- Percepatan benda saat t detik (turunan kedua). Rumusnya ialah:
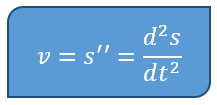
Nah, setelah mengikuti pembahasan mengenai turunan, Sobat Pintar dapat mengerjakan latihan soal-soal turunan pada aplikasi Aku Pintar. Jadi, jangan lupa download aplikasi Aku Pintar di Play Store atau App Store untuk mempelajari materi lengkap mengenai turunan, ya!
DAFTAR PUSTAKA
https://akupintar.id/info-pintar/-/blogs/turunan-fungsi-aljabar-konsep-rumus-dan-aplikasi

Komentar
Posting Komentar