LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

 raisya windriya x ips 3

LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

Aplikasi trigonometri yang sering digunakan dikenal dengan aturan sinus, aturan kosinus, dan luas segitiga. Aturan sinus adalah aturan penting yang berfungsi menghubungkan sisi dan sudut segitiga. Aturan sinus dapat digunakan dalam segitiga apa pun dengan sisi dan sudut berlawanannya diketahui.

Sedangkan aturan kosinus menghubungkan ketiga sisi ke satu sudut. Aturan ini digunakan untuk menjelaskan hubungan antara nilai kosinus dan kuadrat panjang sisi pada salah satu sudut segitiga.

 Aturan Sinus dan Aturan Cosinus merupakan dua aturan yang menghubungkan panjang sisi dan besar sudut dalam segitiga sembarang dengan menggunakan konsep trigonometri. Sesuai dengan namanya, Aturan Sinus melibatkan fungsi sinus, sama halnya dengan Aturan Cosinus. Selain itu, luas segitiga ternyata dapat ditentukan dengan menggunakan bantuan trigonometri, yaitu didasarkan pada besar sudut dan panjang dua sisi yang mengapitnya.

Sedangkan aturan luas segitiga digunakan untuk menentukan luas segitiga jika diketahui sudut apit dan sisi apit dari sebuah segitiga.

Selain aturan sinus dan kosinus, ada juga aturan lain dalam segitiga yang berkaitan dengan luas segitiga. Luas suatu segitiga sembarang dapat dihitung tidak hanya dengan rumus luas segitiga biasa. Namun juga dengan trigonometri.

Aturan Sinus

Terdapat aturan sinus yang perlu diketahui agar memudahkan penghitungan. Berikut rumusnya:

a / Sin A = b / Sin B = c / Sin C

Diketahui segitiga sembarang ABC seperti gambar di bawah ini:

Jawab:

Jika panjang sisi AB = c = 12 cm, dan sisi AC = b cm, diperoleh:

b / Sin B = c / Sin C

b / Sin 45 derajat= 12/Sin 60 derajat

b = 12 Sin 45 derajat / Sin 60 derajat = 12 . 1/2 . √2 dibagi 1/2 √3 = 12√2 / √3

Maka bentuk di atas akan menjadi:

𝑏 = 12√2 / √3 = 12√2 √3 / √3 √3 = 12√6 / 3 = 4√6

Maka, panjang AC = b = 4√6 cm

Aturan Cosinus

Aturan cosinus adalah salah satu aturan dalam trigonometri. Aturan ini menjelaskan hubungan antara kuadrat panjang sisi dengan nilai kosinus dari salah satu sudut dalam sebuah segitiga.

Aturan kosinus digunakan untuk menentukan besar salah satu sudut segitiga saat tiga sisi segitiga diketahui. Selain itu, aturan ini dapat digunakan untuk menentukan salah satu sisi segitiga saat diketahui dua sisi dan sudut apitnya.

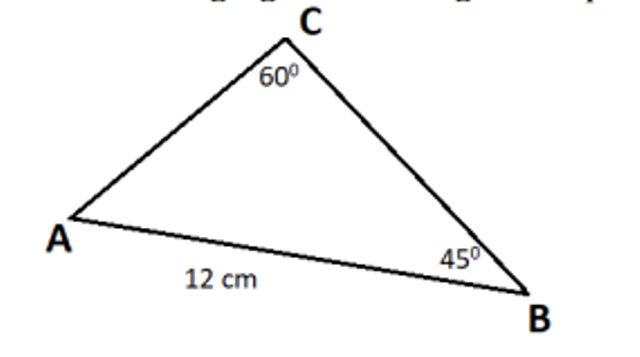
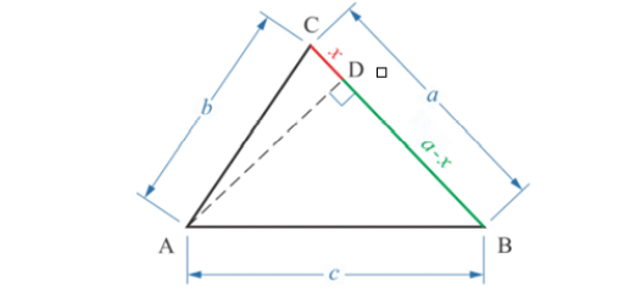
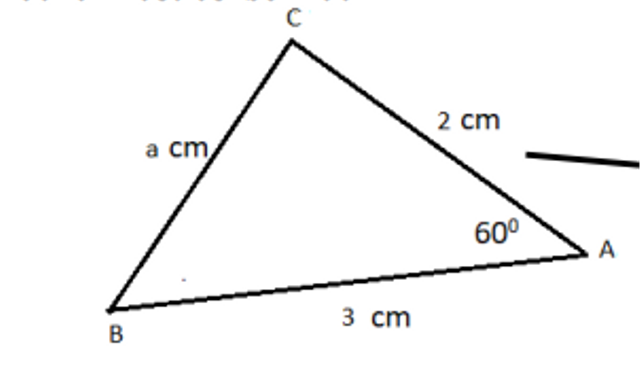
Misalkan panjang AB = c cm; BC = a cm; dan AC = b cm. Jika panjang CD = x cm, panjang BD = (a – x) cm.

Persamaan aturan kosinus ialah 𝑐 2 = 𝑎 2 + 𝑏 2 − 2𝑎𝑏 𝐶𝑜𝑠 𝐶

Contoh soal:

Diketahui segitiga ABC dengan panjang b = 2 cm; c = 3 cm; dan sudut A = 600. Tentukan panjang sisi a?

Dengan menggunakan Aturan Cosinus, maka diperoleh:

𝑎 2 = 2 2 + 3 2 − 2.2.3. 𝐶𝑜𝑠 60 derajat

𝑎 2 = 4 + 9 − 2.2.3. 1 / 2

𝑎 2 = 13 − 6 Maka a = √7

daftar pustaka : https://kumparan.com/kabar-harian/aturan-sinus-dan-cosinus-dalam-sudut-istimewa-trigonometri-1wno1esnnvY/full