Integral fungsi Aljabar
Apa Itu Integral Tak Tentu?
Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.
Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Nah, jika f’(x) dibalik lagi menjadi f(x), maka itu merupakan integral.
Sebelum ke rumus integral tak tentu, elo perlu paham konsep turunan nih. Gue kasih bayangin dikit tentang turunan secara umum.
y= X3 Turunan dari soal ini berapa?
dydx = 3×2 Setelah diturunkan seperti ini, lalu dikali silang.
dy = 3×2 dx
d(X3) = 3×2 dx Bisa dilihat ya, y diganti dengan X3
Nah, dari sini bisa kita simpulkan ya cara mencari turunan bentuknya akan seperti ini nih.
Turunan dari X2 akan menjadi d(X2) = 2x dx
Oke, konsep turunan udah ingat lanjut ke materi integral tak tentu lagi.
Coba deh elo perhatikan antara turunan dan integral di bawah ini.
Turunan:
Sekarang kita balik, dikalikan silang ya:
df(x) = f’(x)dx
Kita tambahkan aja lambang integral (∫), menjadi:
∫df(x) = ∫f’(x)dx
∫f’(x)dx = f(x)+C
Pengertian integral tak tentu (indefinite integral) merupakan suatu fungsi baru yang punya turunan dari fungsi aslinya dan fungsi tersebut belum memiliki nilai pasti. Itulah mengapa dalam integral tak tentu ada konstanta (C).
Rumus Integral Tak Tentu
Oke, kita tahu kalau integral tak tentu berarti nilai atau batasannya belum pasti, sehingga ada nilai konstanta di dalamnya. Sekarang, mari kita definisikan seperti apa sih rumus dasar integral tak tentu? Perhatikan rumus di bawah ini.
Rumus Integral tak tentu:
Supaya lebih mudah dipahami, gue langsung cemplung angka-angkanya ke rumus di atas ya.
Nah, jelas ya sekarang? Jadi, elo hanya perlu memasukkan angka-angkanya ke dalam template rumus di atas. Sampai sini udah mulai paham dikit-dikit lah ya, tapi sebelum buru-buru ke contoh soal integral tak tentu, simak dulu sifat-sifatnya.
Sifat-Sifat Integral Tak Tentu
Pengertian udah tahu, rumus juga elo udah tahu, kurang lengkap rasanya kalau kita gak mengenal sifat-sifat dari integral tak tentu. Berikut adalah sifat-sifat integral tak tentu:

Contoh Soal Integral
Soal 1
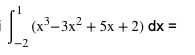
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi 3x2 + 5x + 2 menjadi seperti di bawah ini.
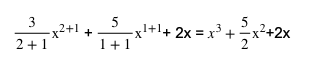
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.
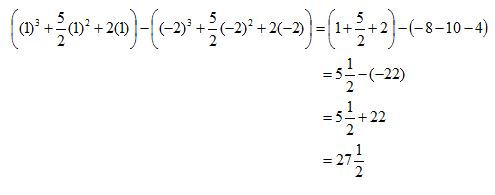
Hasil dari integral tersebut adalah 27,5.
Soal 2.
Diketahui turunan y = f(x) adalah = f ‘(x) = 2x + 3
Jika kurva y = f(x) lewat titik (1, 6), maka tentukan persamaan kurva tersebut.
Jawab:
f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.
Kurva melalui titik (1, 6), berarti f(1) = 6 hingga dapat di tentukan nilai c, yakni 1 + 3 + c = 6 ↔ c = 2.
Maka, persamaan kurva yang dimaksud yaitu:
y = f(x) = x2 + 3x + 2.
Soal 3.
Carilah hasil dari ʃ21 6x2 dx !
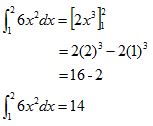
Jadi, hasil dari ʃ21 6x2 dx adalah 14.
Teknik Pengintegralan: Metode Substitusi
Dalam menyelesaikan masalah integral tak tentu, masalah yang ada harus dibawa ke salah satu atau beberapa bentuk integrand yang telah dikenal. Dengan memasukkan atau mensubstitusi variabel baru yang tepat sehingga bentuk yang tadinya belum dikenal primitifnya berubah menjadi bentuk yang telah dikenal.
Diberikan fungsi |
Untuk membuktikan hal tersebut, maka cukup ditunjukkan bahwa derivatif kedua ruang terhadap merupakan fungsi yang sama. Diperhatikan bahwa
Sementara di lain pihak, diperoleh:
Dengan demikian, terbukti bahwa
Contoh.
- Akan ditentukan nilai integral tertentu dari
, untuk suatu konstanta
.
Penyelesaian:
Diambil substitusiatau
maka
. Dengan demikian,
Diperhatikan bahwa nilai
merupakan bentuk intergal yang telah dikenal.
- Akan ditentukan nilai integral tertentu dari
.
Penyelesaian:
Dengan substitusimaka diperoleh
, sehingga diperoleh integrasi:
Diperhatikan bahwa nilai
merupakan bentuk integral yang telah dikenal.
- Tentukan
.
Penyelesaian:
Disubstitusikan, sehingga diperoleh
. Akibatnya,
Contoh Soal Integral Beserta Jawaban dan Pembahasannya
1) Hitunglah integral dari 4x3 – 3x2 + 2x – 1 !

Jadi, integral dari 4x3 – 3x2 + 2x – 1 adalah x4 – x3 + x2 – x + c
2) Tentukan integral dari (x – 2)(2x + 1) !

Jadi, integral dari (x – 2)(2x + 1) adalah 2/3 x3 – 3/2 x2 – 2x + c.
3) Diketahui fungsi y = f(x) memiliki f ‘(x) = 4x + 6. Misal kurva y = f(x) melalui titik (2, 8). Tentukan persamaan kurva tersebut.
f(x) = ʃ f ‘(x), dan f ‘(x) = 4x + 6, maka
f(x) = ʃ (4x + 6) dx
f(x) = 2x2 + 6x + c
Karena kurva melalui titik (2, 8), maka f(2) = 8. Dengan mensubstitusikan ke f(x), diperoleh
f(x) = 2x2 + 6x + c
f(2) = 2(2)2 + 6(2) + c
8 = 8 + 12 + c
c = -12
Jadi, persamaan kurva tersebut adalah y = f(x) = 2x2 + 6x – 12
DAFTAR PUSTAKA
https://www.zenius.net/blog/integral-tak-tentu
https://www.seputarpengetahuan.co.id/2020/05/integral-tak-tentu.html

Komentar
Posting Komentar