nama : raisya windriya

kelas : X IPS 3

NILAI MUTLAK

Nilai mutlak merupakan suatu jarak antara bilangan tertentu dengan nol pada garis bilangan real. Karena jarak, maka nilainya selalu positif (tidak ada yang negatif). Sehingga nilai mutlak yaitu nilai yang selalu positif.

Konsep nilai mutlak digunakan pada Selisih bilangan selalu dianggap positif karena itu konsep nilai mutlak berlaku (digunakan) pada hitungan selilih bilangan.

Jarak suatu benda selalu dianggap positif karena konsep nilai mutlak digunakan pada hitungan jarak benda, Toleransi resistor (perubahan nilai resistansi), begitu juga dengan galat pengukuran juga menggunakan konsep nilai mutlak.


Secara formal, nilai mutlak x didefinisikan dengan

Atau bisa ditulis :

| x | = -x jika x ≥ 0
| x | = -x jika x < 0

Definisi diatas bisa di maknai sebagai berikut :

  • Nilai mutlak bilangan positif ataupun nol ialah bilangan itu sendiri
  • Nilai mutlak bilangan negatif yaitu lawan dari bilangan tersebut


Contohnya:
| 7 | = 7 | 0 | = 0 | -4 | = -(-4) = 4
Maka, jelas bahwasanya nilai mutlak tiap bilangan real akan selalu memiliki nilai positif atau nol.

Persamaan √x2=x bernilai benar jika x ≥ 0. Untuk x < 0, maka √x2=−x. Bisa kita tulis

Jika di perhatikan, bentuk diatas sama persis dengan definisi nilai mutlak x.

Oleh sebab itu, pernyataan berikut benar untuk setiap x bilangan real.

|x|=√x2 Andai kedua ruas persamaan diatas di kuadratkan bisa didapat |x|2=x2 Persamaan terakhir ini berupa konsep dasar penyelesaian persamaan ataupun pertidaksamaan nilai mutlak dengan cara menguadratkan kedua ruas.

Seperti yang di lihat, tanda mutlak akan hilang jika dikuadratkan.


Contoh soal Nilai Mutlak :


Contoh 1
Tentukanlah  himpunan penyelesaian  |2x – 7| = 3

Jawaban :
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)

Contoh 2

Tentukanlah  himpunan penyelesaian |4x + 2| ≥ 6

Jawaban :
|4x + 2| ≥ 6 (4x + 2 ≤ -6 atau 4x + 2 ≥ 6)
|4x + 2| ≥ 6 (4x ≤ -8 atau 4x ≥ 4)
|4x + 2| ≥ 6 (x ≤ -2 atau x ≥ 1)

Maka, HP = (x ≤ -2 atau x ≥ 1)


DAFTAR PUSTAKA

Alika, Raisya Windriya. 2021. "Contoh soal Nilai Mutlak", https://rumusrumus.com/contoh-soal-nilai-mutlak/, diakses pada 3 Agustus 2021 pukul 11.21.




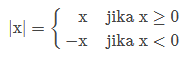
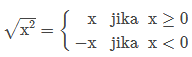
Komentar

Posting Komentar

Postingan populer dari blog ini

Gambar
 raisya windriya x ips 3                      koordinat kutub dan koordinat kartesius Koordinat kutub merupakan koordinat yang ada di koordinat cartesius yang terletak pada suatu lingkaran x^2 + y^2 = r^2 sehingga koordinat kutib ditulis berdasarkan jari-jari lingkaran (r) dan sudut yang dibentuk terhadap sumbu X positif. Misalkan koordinat cartesius A adalah (x,y), dan koordinat kutub titik A adalah (r,α), hubungan kedua titik adalah :  x = r cos α  dan y = r sin α CONTOH SOAL JARAK DUA TITIK KOORDINAT KUTUB  Untuk menghitung jarak dua titik koordinat kutub, caranya menggunakan jarak dua titik pada koordinat cartesius. Artinya kita harus mengubah dulu koordinat kutub menjadi koordinat cartesius. Untuk jarak dua titik koordinat cartesius, CONTOH SOAL daftar pustaka  https://www.konsep-matematika.com/2015/11/koordinat-kutub-dan-koordinat-cartesius-pada-trigonometri.html
Baca selengkapnya

Barisan dan Deret

Gambar
 A.  Baris dan Deret Aritmatika Barisan adalah daftar bilangan yang dituliskan secara berurutan dari kiri ke kanan, di mana ia mempunyai pola atau karakteristik bilangan tertentu. Barisan biasanya disimbolkan dengan Un; Sedangkan deret adalah penjumlahan dari suku-suku yang ada di dalam suatu barisan tertentu. Deret ini biasanya disimbolkan dengan Sn; Kemudian aritmetika adalah ilmu berhitung dasar yang mencakup penjumlahan, pengurangan, perkalian, dan pembagian, yang ada di dalam cabang ilmu pengetahuan matematika. Psstt, inget lho, ejaan yang benar itu ‘aritmetika’, bukan ‘aritmatika’. Rumus : a a+b  a+2b a+3b Lebih lanjut, selisih antara nilai suku-suku saling berdekatan dan selalu sama, yaitu b. Misalnya: Un – U(n-1) = b Sebagai contoh baris 1, 3, 5, 7, 9, merupakan baris aritmetika dengan nilai: b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2 Sementara itu, deret aritmetika adalah suatu penjumlahan antar suku-suku dari sebuah barisan aritmetika. Untuk penjumlahan dari ...
Baca selengkapnya
Gambar
 raisya windriya x ips 3 LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA , GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN Luas Segi n Beraturan   Pada segi n beraturan Setiap segi n beraturan bisa kita bagi menjadi n buah segitiga yang kongruen Setiap titik sudut pada segi n beraturan bisa dilalui sebuah lingkaran, lingkaran ini disebut lingkaran luar segi n. Semuat titik sudut akan dilewati lingkaran (tidak ada yang tertinggal).   Menghitung luas segi n beraturan akan lebih mudah jika diketahui jari-jari lingkaran luarnya Setiap segi n bisa dibagi menjadi n buah segitiga yang kongruen seperti pada gambar di atas. Selanjutnya kita ambil salah satu segitiganya Besar sudut A adalah  Luas segitiga adalah LΔ = ½ .R.R sin A Luas segi n beraturan adalah L n  = n. LΔ Rumus ini merupakan rumus luas segi n beraturan yang diketahui jari-jari lingkaran luarnya.   Bagaimana jika diketahui sisinya ? Pertama kita cari dulu hubungan antara ja...
Baca selengkapnya